Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- CarouselCollectionview
- class struct
- Carousel CollectionView
- wil
- tableview section별 다른 cell적용
- 테이블뷰 나누기
- CoreData
- firebase
- 프로그래머스
- UserDefaults
- Reference Cycle
- coremotion
- NavigationSearchBar
- TableView
- 면접을 위한 CS 전공 지식 노트 Tree
- TableView Section
- til
- Input Output
- SWIFT
- Value Type Reference Type
- @escaping
- retain cycle
- ReferceCycle
- 자료구조
- 양궁대회
- UIKit
- Array vs Linked List
- 면접을 위한 CS전공 지식 노트
- 롤케이크 자르기
- 강한 참조 순환
Archives
- Today
- Total
개발하는 동글 :]
[자료구조] Graph 본문
그래프 용어 정리

정점(Vertex) 노드(node) 라고도 하며 정점에는 데이터가 저장된다. (0, 1, 2, 3)
| 간선(Edge) | 정점(노드)를 연결하는 선으로 link, branch 라고도 부른다. |
| 인접 정점(adjacent Vertex) | 간선에 의해 직접 연결된 정점(0과 2은 인접정점) |
| 단순 경로(simple path) | 경로 중에서 반복되는 정점이 없는 경우. 한붓그리기와 같이 같은 간선을 지나가지 않는 경로 ( 0->3->2->1 은 단순경로 ) |
| 차수(degree) | 무방향 그래프에서 하나의 정점에 인접한 정점의 수 (0의 차수는 3) |
| 진출 차수(in-degree) | 방향 그래프에서 외부로 향하는 간선의 수 |
| 진입 차수(out-degree) | 방향 그래프에서 외부에서 들어오는 간선의 수 |
| 경로 길이(path length) | 경로를 구성하는데 사용된 간선의 수 |
| 사이클(cycle) | 단순 경로의 시작 정점과 종료 정점이 동일한 경우 |
그래프
그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조이다.
정확히는 정점(Vertex)간의 관계를 표현하는 조직도라고 볼 수 있다. 이러한 면에서 트리는 그래프의 일종인 셈이다.
하지만 그래프는 트리와는 달리 정점마다 간선이 있을 수도 있고 없을 수도 있으며, 루트노드와 부모와 자식이라는 개념이 존재하지 않는다.
그래프의 종류
무방향 그래프 [Undirected Graph]
- 무방향 그래프의 간선은 간선을 통해서 양 방향으로 갈 수 있다.
- 정범 A와 정점 B를 연결하는 간선은 (A,B)와 같이 정점의 쌍으로 표현한다.
방향그래프 [Directed Graph]
- 간선에 방향성이 존재하는 그래프
- A -> B로만 갈 수 있는 간선은 <A,B>로 표시한다.
가중치 그래프[Weighted Graph]
- 간선에 비용이나 가중치가 할당된 그래프
- 네트워크라고도 한다.
연결 그래프 [Connected Graph]
- 모든 두 꼭짓점 사이에 경로가 존재하는 그래프
- 무방향 그래프에 있는 모든 정점쌍에 대해서 항상 경로가 존재하는 경우
- ex) 트리구조(Tree): 사이클을 가지지않는 특징을 가지고 있는 연결 그래프
비연결 그래프[Disconnected Graph]
- 무방향 그래프에서 특정 정점쌍 사이에 경로가 존재하지 않는 경우
사이클 [Cycle]
- 단순 경로의 시작 정점과 종료 정점이 동일한 경우 (결국 순환한다는 내용)
- 단순 경로 : 경로 중에서 반복되는 정점이 없는 경우
비순환 그래프[Acylic Graph]
- 사이클이 없는 그래프이다. (순환하지 않는 그래프)
완전 그래프[Complete Graph]
- 그래프에 속해 있는 모든 정점이 서로 연결 되어있는 그래프.
- 무방향 완전 그래프 (한곳으로 향하는데 모두 연결되어 있는 그래프)
- 정점의수가 = n 이면 // 간선의수는 n*(n-1) /2 가 된다.
그래프 구현
1. 인접행렬 방식
- 인접행렬 방식인접행렬은 그래프의 노드를 2차원 배열로 만든 것이다.노드들 간에 직접 연결이 되어있으면 1을, 아니면 0을 넣어서 행렬을 완성시킨 것이다.
인접행렬의 장점
- 2차원 배열 안에 모든 정점들의 간선 정보가 담겨있기 때문에 두 정점에 대한 연결 정보를 조회할 때 O(1) 의 시간복잡도면 가능하다.
- 인접리스트에 비해 구현이 쉽다.
인접행렬의 단점
- 모든 정점에 대해 간선 정보를 대입해야 하므로 O(n^2) 의 시간복잡도가 소요된다.
- 무조건 2차원 배열이 필요하기 때문에 필요 이상의 공간이 낭비된다.
2. 인접리스트 방식
- 인접리스트는 그래프의 노드를 리스트로 표현한 것이다.
- 주로 정점의 리스트 배열을 만들어 관계를 설정하며 노드들 간에 직접 연결이 되어있으면 해당 노드의 인덱스에 그 노드를 삽입해주면 된다.
- 즉, 1에는 2와 3이 직접 연결되어 있기 때문에 배열의 1번째 칸에 2와 3을 넣어준다.
인접리스트의 장점
- 정점들의 연결 정보를 탐색할 때 O(n) 시간이면 가능하다.
- 필요한 만큼의 공간만 사용하기 때문에 공간의 낭비가 적다.
인접리스트의 단점
- 특정 두 점이 연결되었는지 확인하려면 인접행렬에 비해 시간이 오래걸린다. (O(E) 시간 소요. E는 간선의 개수)
- 구현이 비교적 어렵다.
그래프 탐색
1. 깊이우선탐색(Depth-First Search, DFS)
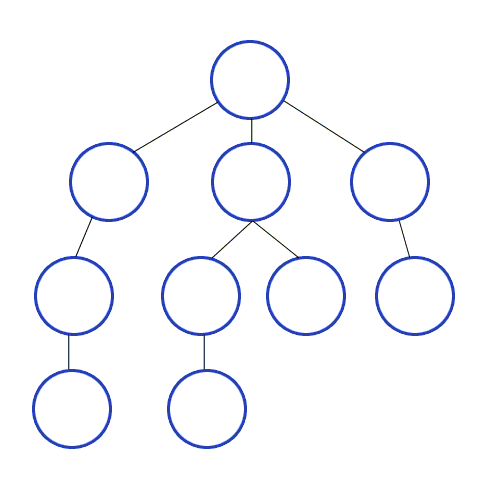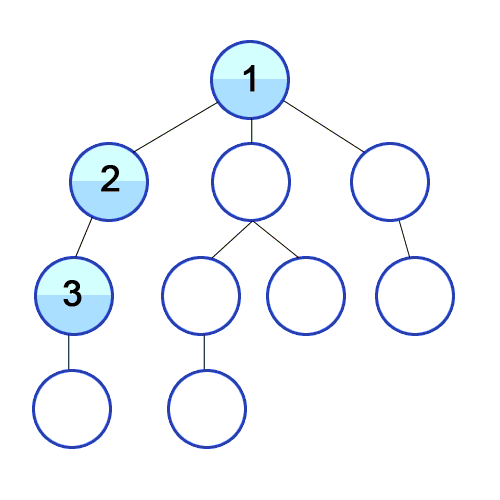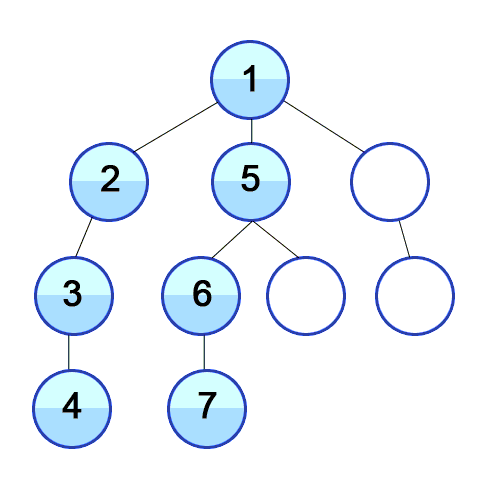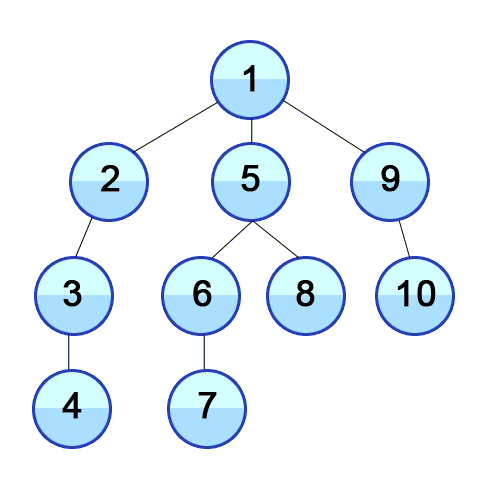
- 그래프의 시작점에서 다음 브랜치로 넘어가기 전에, 해당 브랜치를 모두 탐색
- 재귀 혹은 스택 통해 탐색을 수행하고 더 이상 연결된 간선이 없을때까지 탐색하면 다시 되돌아가 연결된 정점을 탐색
- 시간 복잡도
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(V+E)
- 메모리 효율 : 인접리스트 > 인접행렬
- 조회 속도 : 인접리스트 < 인접행렬
2. 너비우선탐색(Breadth-First Search, BFS)
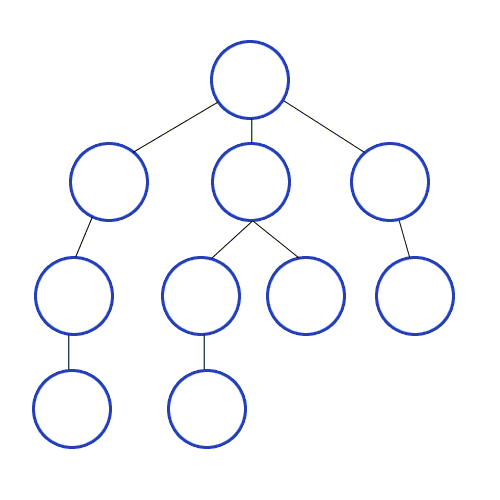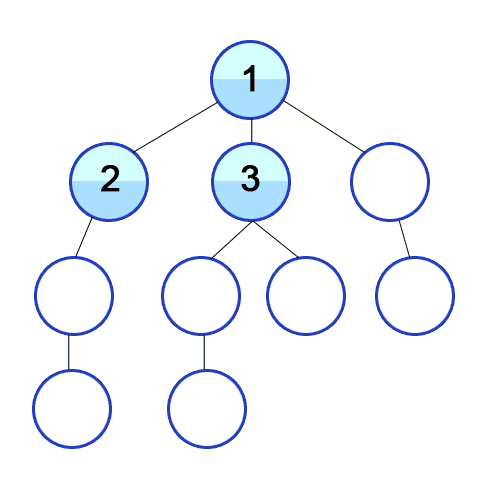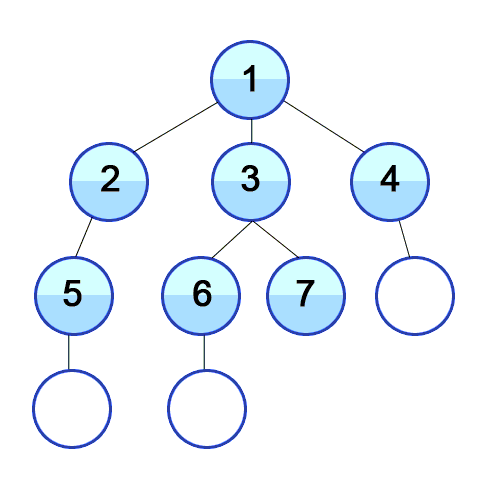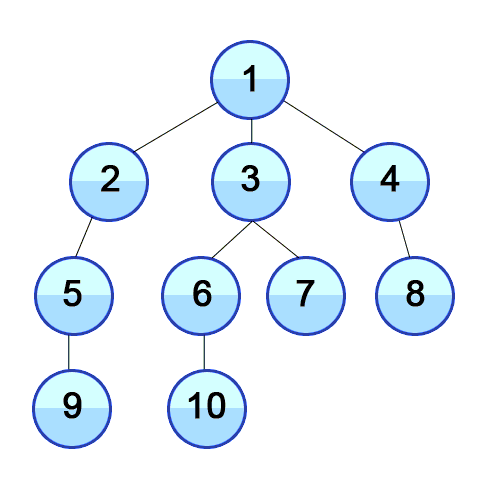
- BFS는 너비 우선 탐색이라고 불리며 그 이유는 그래프의 시작점에서 (너비가) 가까운 점들부터 우선적으로 탐색
- 알고리즘 개요는 시작점을 큐(queue)에 넣은 뒤에, 큐에 아무런 요소가 없을때까지 ****인접한 정점들을 탐색해 나아가면 진행
- 시간 복잡도
- 인접 행렬 : O(V^2)
- 인접 리스트 : O(V+E)
Minimum Spanning Tree
- 최소신장트리(Minimum Spanning Tree)는 특정 그래프의 신장트리 중에 가장 최소의 weight을 가지는 신장트리를 뜻한다.
- 신장트리(Spanning Tree)는 그래프가 있을 때 모든 노드를 포함하면서 사이클이 존재하지 않는 최소 연결 부분 그래프를 의미한다.
- 최소신장트리를 만드는 알고리즘은 대표적으로 두가지가 있는데, 두 알고리즘 모두 그리디 알고리즘으로, 탐욕적 방법으로 최적해를 찾아내는 것을 보장한다.
- 두 알고리즘은 크루스칼(Kruskal) 프림(Prim) 알고리즘이다.
Kruskal 알고리즘
크루스칼 알고리즘은 set A를 forest, 즉 독립적인 트리의 집합으로 본다. 각 노드를 single node tree로 보고, 이 forest안에서 두개의 트리를 연결하는 edge 중에 least-weight edge를 찾아서 연결한다.
- 간선 데이터를 비용에 따라 오름차순 정렬
- 간선을 하나씩 확인하며 현재의 간선이 사이클을 발생시키는지 확인한다.i. 사이클이 발생하지 않는 경우, 최소신장트리에 포함ii. 사이클이 발생할 경우, 최소신장트리에 포함 x
- 모든 간선에 대해 2. 반복
Prim 알고리즘
프림 알고리즘은 set A가 single tree을 형성한다. 노드 각각을 독립적인 트리로 보지 않고, 하나의 tree를 구성하고 이를 확장시키면서 MST를 구성하는 알고리즘이다.
- 시작 정점을 MST에 추가한다.
- MST set에 인접한 노드들 중에 최소 비용을 가지는 간선으로 연결된 노드를 선택하여 MST에 추가한다.
- MST가 V-1개의 간선을 가질때까지 반복한다.
