Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 양궁대회
- 프로그래머스
- NavigationSearchBar
- Value Type Reference Type
- til
- UIKit
- 자료구조
- coremotion
- Array vs Linked List
- @escaping
- UserDefaults
- CoreData
- Reference Cycle
- SWIFT
- Input Output
- 롤케이크 자르기
- ReferceCycle
- firebase
- tableview section별 다른 cell적용
- CarouselCollectionview
- 면접을 위한 CS 전공 지식 노트 Tree
- TableView Section
- 테이블뷰 나누기
- TableView
- retain cycle
- 면접을 위한 CS전공 지식 노트
- class struct
- wil
- 강한 참조 순환
- Carousel CollectionView
Archives
- Today
- Total
개발하는 동글 :]
[자료구조] Tree 본문
트리
- 트리는 그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져 있고, 트리 구조로 배열된 일종의 계층적 데이터의 집합입니다. 루트 노드, 리프 노드 등으로 구성
- 트리로 이루어진 집합을 숲이라고 합니다.
트리의 특징
- 부모, 자식 계층 구조
- V - 1 = E라는 특징이 있습니다. 간선 수는 노드 수 - 1
- 임의의 두 노드 사이의 경로는 유일무이 하게 존재 한다. 즉 트리 내의 어떤 노드와 어떤 노드까지의 경로는 반드시 존재
트리의 구성

- 정점(Vertex): 자료를 보관하는 단위, 노드(Node)라고 부름
- 간선(Edge): 정점에서 다른 정점으로 가는 경로, 링크(Link, 다른 노드의 위치 정보) 혹은 가지(Branch)로 부름
- 루트 노드 : 가장 위에 있는 노드
- 내부 노드 : 루트 노드와 내부 노드 사이에 있는 노드를 뜻함
- 리프 노드 : 자식 노드가 없는 노드
트리의 높이와 레벨

- 깊이 : 루트 노드부터 특정 노드까지 최단 거리로 갔을 때의 거리
- 높이 : 루트 노드부터 리프 노드까지 거리 중 가장 긴 거리
- 레벨 : 깊이와 같은 의미
- 서브트리 : 트리 내의 하위 집합
이진 트리
- 이진 트리는 자식의 노드 수가 두 개 이하인 트리를 의미하며, 이를 다음과 같이 분류

- 정이진 트리(full binary tree) : 자식 노드가 0 또는 두 개인 이진 트리
- 완전 이진 트리(complete binary tree) : 왼쪽에서부터 채워져 있는 이진 트리, 마지막 레벨을 제외하고 모든 레벨이 채워져 있으며, 마지막 레벨의 경우 왼쪽부터 채워져 있음
- 변질 이진 트리(degenerate binary tree) : 자식 노드가 하나밖에 없는 이진 트리
- 포화 이진 트리(perfect binary tree) : 모든 노드가 꽉 차 있는 이진 트리
- 균형 이진 트리(balaned binary tree) : 왼쪽, 오른쪽 노드의 높이 차이가 1 이하인 이진 트리
- map, set을 구성하는 레드 블랙 트리는 균형 이진 트리 중 하나
이진 탐색 트리[BST]

- 이진 탐색 트리는 노드의 오른쪽 하위 트리에는 “노드 값보다 큰 값”이 있는 노드만 포함되고, 왼쪽 하위 트리에는 “노드 값보다 작은 값”이 들어 있는 트리
- 검색을 하기에 용이하다.
- 보통 요소를 찾을 때 O(log n) 최악의 경우 O(n) 이유는 삽입 순서에 따라 선형적일 수 있기 때문이다.

AVL 트리[Adelson - Velsky and Landis tree]
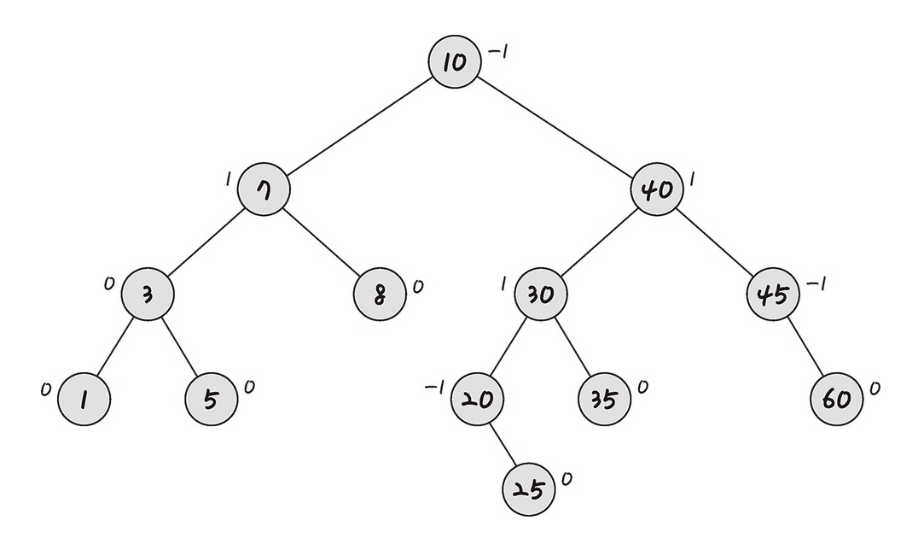
- 앞서 설명한 최악의 경우 선형적인 트리가 되는 것을 방지하고 스스로 균형을 잡는 이진 탐색 트리
- 두 자식 서브트리의 높이는 항상 최대 1만큼 차이남
- 탑색, 삽입, 삭제, 모두 O(log n) 소요
- 삽입, 삭제를 할 때마다 균형이 안 맞는 것을 맞추기 위해 트리 일부를 왼쪽 혹은 오른쪽으로 회전 시켜며 균형을 잡음
